Unique Values in Python: A Benchmark

An interesting question came up in the development of Yellowbrick: given a vector of values, what is the quickest way to get the unique values? Ok, so maybe this isn’t a terribly interesting question, however the results surprised us and may surprise you as well. First we’ll do a little background, then I’ll give the results and then discuss the benchmarking method.

The problem comes up in Yellowbrick when we want to get the discrete values for a target vector, y — a problem that comes up in classification tasks. By getting the unique set of values we know the number of classes, as well as the class names. This information is necessary during visualization because it is vital in assigning colors to individual classes. Therefore in a Visualizer we might have a method as follows:

class ScatterVisualizer(Visualizer):

    def fit(X, y=None):
        labels = [
            str(item) for item in set(y)
        ]

        colors = dict(zip((labels, resolve_colors(len(labels)))))
        ...

NOTE: a related question is how can we determine a continuous vector y (a regression problem) from a categorical vector y (a classification problem) automatically? This allows us to assign a sequential vs. discrete colors to the target variable.

To make a short story even shorter, when I reviewed the above code, my response was: “isn’t something like np.unique faster?”. I was returned a simple “yep, sure is” answer, and the code was changed to np.unique — job done, right? When the commit was pushed, a few tests didn’t pass; it looked like there was an issue converting a Python data type into the numpy data type to pass to the unique function (turns out this was not the issue), but that caused me to investigate the input type to the uniqueness method. Using set vs. np.unique depends on if the input type is a Python list or a Numpy array, as we’ll see shortly.

So let’s get into results. We proposed three methods of getting the unique items from our target vector:

import numpy as np
from sklearn.preprocessing import LabelEncoder


def py_unique(data):
    return list(set(data))


def np_unique(data):
    return np.unique(data)


def sk_unique(data):
    encoder = LabelEncoder()
    encoder.fit(data)
    return encoder.classes_

The first converts a Python set into a list and returns the unsorted list of unique values. The second uses numpy and converts the input into a np.array; it actually returns a sorted array of values. The third option is more directly related to Scikit-Learn, fitting a LabelEncoder transformer and getting the unique classes from that.

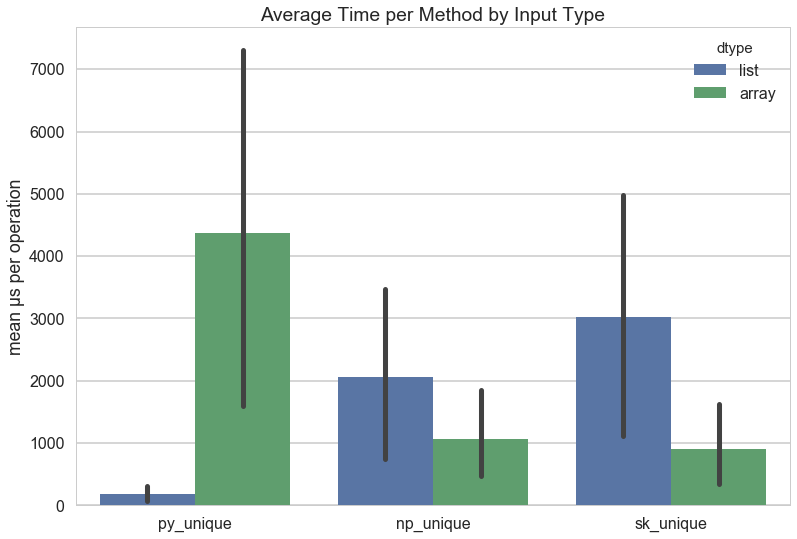
Before getting into the benchmarking methodology, the results are as follow:

The results in the above figure show that by far the fastest unique computation is using set on a Python list. This is especially surprising given the fact that numpy arrays are C implementations, and are therefore guaranteed to be blazingly fast. Using np.unique is on average faster than everything else, and it certainly gives the best performance on array data structures out of all the methods. It does slightly worse with Python lists, but not as badly as Python does with array structures. Scikit-Learn clearly adds some overhead, especially when it comes to Python lists, but performs fairly well for array structs.

In the end, we chose to stick with np.unique in Yellowbrick, primarily because the expected input is in fact a np.array, either from data loaded from np.loadtxt or from a Pandas Series or DataFrame. If a Python list is passed in, then the performance is adequate for our needs. Still, the performance gaps based on input type were a surprise and I would encourage you, as always, to benchmark code and not just rely on traditional assumptions!

NOTE: If you believe that our implementation or benchmarking can be improved, please let me know!

Benchmarking Notes

Benchmarking, especially in Python, is a tricky task. Therefore, in order to be as transparent as possible in the claims made above and to quickly catch any mistakes, I present the benchmarking methodology here. The complete script and notebook can be found on Gist.

First, I will say that I did explore the timeit module for benchmarking, but couldn’t make these particular tests work with it. Instead, I wrote a simple timing function that returns the time delta in microseconds (μs). I also wrote a benchmark function that applied the unique method to a dataset n=10000 times and returned the average time for an operation.

def timeit(func):
    start = time.time()
    func()
    return ((time.time() - start) * 1000000.0)


def benchmark(func, data, n=10000):
    delta = sum([
        timeit(lambda: func(data))
        for _ in range(n)
    ])

    return (float(delta) / float(n))

Because a set operation is at worst O(n) and therefore depends on the length of the dataset, I created a function to make a dataset of a variable length with between 1 and 52 unique elements. This data was then stored as a Python list or as a Numpy array object depending on the input tested.

def make_data(uniques=10, length=10000):
    chars = string.ascii_letters
    if uniques > len(chars):
        raise ValueError("too many uniques for the choices")

    return [
        random.choice(chars[:uniques])
        for idx in range(length)
    ]

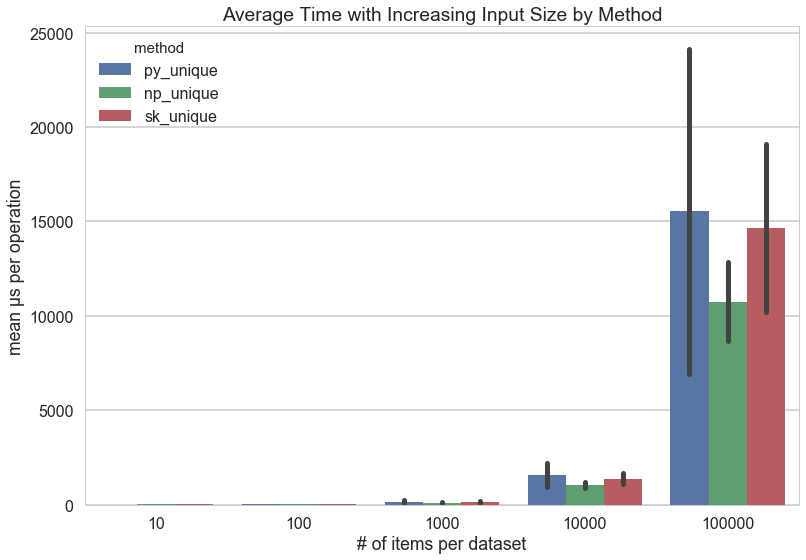
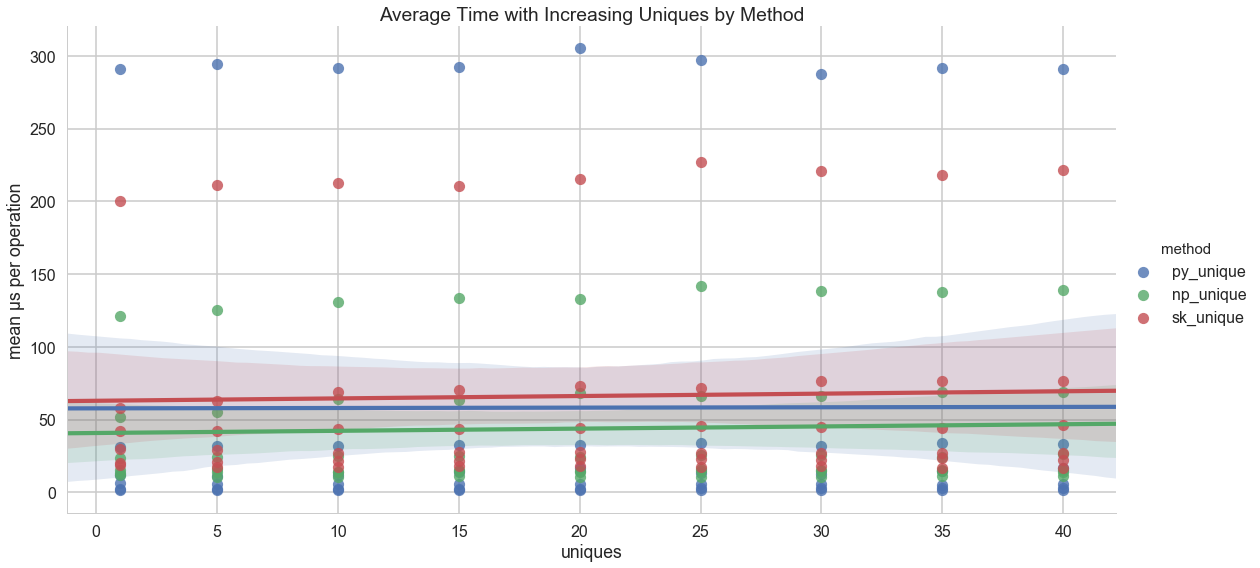
The actual test protocol ran on datasets whose length went from 10 to 100,000 items by a factor of ten each time (e.g. 10, 100, 1000, etc.). The test also factored different numbers of unique values from 1 to 40 by 5. Each dataset was then benchmarked as a list and an array against the three _unique methods for a total of 195 benchmarks.

As you can see, the amount of time per operation increases exponentially as the length of the dataset increases:

And it appears (as expected) that the number of unique values per dataset does not have a meaningful impact on the operation time:

Hopefully these timing numbers and approach to benchmarking seem valid. They certainly work to highlight interesting places where our coding assumptions might fail us.

Benchmarking Notes#

Benchmarking Notes